Неопределенный и определенный интегралы. Интегралы для чайников: как решать, правила вычисления, объяснение
Определенный интеграл. Примеры решений
И снова здравствуйте. На данном уроке мы подробно разберем такую замечательную вещь, как определенный интеграл. На этот раз вступление будет кратким. Всё. Потому что снежная метель за окном.
Для того чтобы научиться решать определенные интегралы необходимо:
1) Уметь находить неопределенные интегралы.
2) Уметь вычислить определенный интеграл.
Как видите, для того чтобы освоить определенный интеграл, нужно достаточно хорошо ориентироваться в «обыкновенных» неопределенных интегралах. Поэтому если вы только-только начинаете погружаться в интегральное исчисление, и чайник еще совсем не закипел, то лучше начать с урока Неопределенный интеграл. Примеры решений . Кроме того, есть pdf-курсы для сверхбыстрой подготовки – если у вас в запасе буквально день, пол дня.
В общем виде определенный интеграл записывается так:
Что прибавилось по сравнению с неопределенным интегралом? Прибавились пределы интегрирования .
Нижний предел интегрирования
Верхний предел интегрирования
стандартно обозначается буквой .
Отрезок называется отрезком интегрирования
.
Прежде чем мы перейдем к практическим примерам, небольшое faq по определенному интегралу.
Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти число.
Как решить определенный интеграл? С помощью знакомой со школы формулы Ньютона-Лейбница :

Формулу лучше переписать на отдельный листочек, она должна быть перед глазами на протяжении всего урока.
Этапы решения определенного интеграла следующие:
1) Сначала находим первообразную функцию (неопределенный интеграл). Обратите внимание, что константа в определенном интеграле не добавляется . Обозначение является чисто техническим, и вертикальная палочка не несет никакого математического смысла, по сути – это просто отчёркивание. Зачем нужна сама запись ? Подготовка для применения формулы Ньютона-Лейбница.
2) Подставляем значение верхнего предела в первообразную функцию: .
3) Подставляем значение нижнего предела в первообразную функцию: .
4) Рассчитываем (без ошибок!) разность , то есть, находим число.
Всегда ли существует определенный интеграл? Нет, не всегда.
Например, интеграла не существует, поскольку отрезок интегрирования не входит в область определения подынтегральной функции (значения под квадратным корнем не могут быть отрицательными). А вот менее очевидный пример: . Такого интеграла тоже не существует, так как в точках , отрезка не существует тангенса. Кстати, кто еще не прочитал методический материал Графики и основные свойства элементарных функций – самое время сделать это сейчас. Будет здорово помогать на протяжении всего курса высшей математики.
Для того чтобы определенный интеграл вообще существовал, достаточно чтобы подынтегральная функция была непрерывной на отрезке интегрирования .
Из вышесказанного следует первая важная рекомендация: перед тем, как приступить к решению ЛЮБОГО определенного интеграла, нужно убедиться в том, что подынтегральная функция непрерывна на отрезке интегрирования . По студенческой молодости у меня неоднократно бывал казус, когда я подолгу мучался с нахождением трудной первообразной, а когда наконец-то ее находил, то ломал голову еще над одним вопросом: «что за ерунда получилась?». В упрощенном варианте ситуация выглядит примерно так:
 ???! Нельзя подставлять отрицательные числа под корень! Что за фигня?! Изначальная невнимательность.
???! Нельзя подставлять отрицательные числа под корень! Что за фигня?! Изначальная невнимательность.
Если для решения (в контрольной работе, на зачете, экзамене) Вам предложен несуществующий интеграл вроде , то нужно дать ответ, что интеграла не существует и обосновать – почему.
Может ли определенный интеграл быть равен отрицательному числу? Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будет несобственный интеграл , коим отведена отдельная лекция.
Может ли нижний предел интегрирования быть больше верхнего предела интегрирования? Может, и такая ситуация реально встречается на практике.
– интеграл преспокойно вычисляется по формуле Ньютона-Лейбница.
Без чего не обходится высшая математика? Конечно же, без всевозможных свойств. Поэтому рассмотрим некоторые свойства определенного интеграла .
В определенном интеграле можно переставить верхний и нижний предел, сменив при этом знак :

Например, в определенном интеграле перед интегрированием целесообразно поменять пределы интегрирования на «привычный» порядок:
 – в таком виде интегрировать значительно удобнее.
– в таком виде интегрировать значительно удобнее.

 – это справедливо не только для двух, но и для любого количества функций.
– это справедливо не только для двух, но и для любого количества функций.
В определенном интеграле можно проводить замену переменной интегрирования , правда, по сравнению с неопределенным интегралом тут есть своя специфика, о которой мы еще поговорим.
Для определенного интеграла справедлива формула интегрирования по частям
:
Пример 1
Решение:
(1) Выносим константу за знак интеграла.
(2) Интегрируем по таблице с помощью самой популярной формулы ![]() . Появившуюся константу целесообразно отделить от и вынести за скобку. Делать это не обязательно, но желательно – зачем лишние вычисления?
. Появившуюся константу целесообразно отделить от и вынести за скобку. Делать это не обязательно, но желательно – зачем лишние вычисления?
 . Сначала подставляем в верхний предел, затем – нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ.
. Сначала подставляем в верхний предел, затем – нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ.
Пример 2
Вычислить определенный интеграл
Это пример для самостоятельно решения, решение и ответ в конце урока.
Немного усложняем задачу:
Пример 3
Вычислить определенный интеграл![]()
Решение:
(1) Используем свойства линейности определенного интеграла.
(2) Интегрируем по таблице, при этом все константы выносим – они не будут участвовать в подстановке верхнего и нижнего предела.
(3) Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница:![]()
СЛАБОЕ ЗВЕНО в определенном интеграле – это ошибки вычислений и часто встречающаяся ПУТАНИЦА В ЗНАКАХ. Будьте внимательны! Особое внимание заостряю на третьем слагаемом: ![]() – первое место в хит-параде ошибок по невнимательности, очень часто машинально пишут
– первое место в хит-параде ошибок по невнимательности, очень часто машинально пишут ![]() (особенно, когда подстановка верхнего и нижнего предела проводится устно и не расписывается так подробно). Еще раз внимательно изучите вышерассмотренный пример.
(особенно, когда подстановка верхнего и нижнего предела проводится устно и не расписывается так подробно). Еще раз внимательно изучите вышерассмотренный пример.
Следует заметить, что рассмотренный способ решения определенного интеграла – не единственный. При определенном опыте, решение можно значительно сократить. Например, я сам привык решать подобные интегралы так:

Здесь я устно использовал правила линейности, устно проинтегрировал по таблице. У меня получилась всего одна скобка с отчёркиванием пределов:  (в отличие от трёх скобок в первом способе). И в «целиковую» первообразную функцию, я сначала подставил сначала 4, затем –2, опять же выполнив все действия в уме.
(в отличие от трёх скобок в первом способе). И в «целиковую» первообразную функцию, я сначала подставил сначала 4, затем –2, опять же выполнив все действия в уме.
Какие недостатки у короткого способа решения? Здесь всё не очень хорошо с точки зрения рациональности вычислений, но лично мне всё равно – обыкновенные дроби я считаю на калькуляторе.
Кроме того, существует повышенный риск допустить ошибку в вычислениях, таким образом, студенту-чайнику лучше использовать первый способ, при «моём» способе решения точно где-нибудь потеряется знак.
Однако несомненными преимуществами второго способа является быстрота решения, компактность записи и тот факт, что первообразная находится в одной скобке.
Совет: перед тем, как использовать формулу Ньютона-Лейбница, полезно провести проверку: а сама-то первообразная найдена правильно?
Так, применительно к рассматриваемому примеру: перед тем, как в первообразную функцию подставлять верхний и нижний пределы, желательно на черновике проверить, а правильно ли вообще найден неопределенный интеграл? Дифференцируем:
Получена исходная подынтегральная функция, значит, неопределенный интеграл найден верно. Теперь можно и формулу Ньютона-Лейбница применить.
Такая проверка будет не лишней при вычислении любого определенного интеграла .
Пример 4
Вычислить определенный интеграл
Это пример для самостоятельно решения. Попробуйте решить его коротким и подробным способом.
Замена переменной в определенном интеграле
Для определенного интеграла справедливы все типы замен, что и для неопределенного интеграла. Таким образом, если с заменами у Вас не очень, следует внимательно ознакомиться с уроком Метод замены в неопределенном интеграле .
В этом параграфе нет ничего страшного или сложного. Новизна состоит в вопросе, как поменять пределы интегрирования при замене .
В примерах я постараюсь привести такие типы замен, которые еще нигде не встречались на сайте.
Пример 5
Вычислить определенный интеграл
Главный вопрос здесь вовсе не в определенном интеграле, а в том, как правильно провести замену. Смотрим в таблицу интегралов
и прикидываем, на что у нас больше всего похожа подынтегральная функция? Очевидно, что на длинный логарифм: ![]() . Но есть одна неувязочка, в табличном интеграле под корнем , а в нашем – «икс» в четвёртой степени. Из рассуждений следует и идея замены – неплохо бы нашу четвертую степень как-нибудь превратить в квадрат. Это реально.
. Но есть одна неувязочка, в табличном интеграле под корнем , а в нашем – «икс» в четвёртой степени. Из рассуждений следует и идея замены – неплохо бы нашу четвертую степень как-нибудь превратить в квадрат. Это реально.
Сначала готовим наш интеграл к замене:

Из вышеуказанных соображений совершенно естественно напрашивается замена:
Таким образом, в знаменателе будет всё хорошо: .
Выясняем, во что превратится оставшаяся часть подынтегрального выражения, для этого находим дифференциал :
![]()
По сравнению с заменой в неопределенном интеграле у нас добавляется дополнительный этап.
Находим новые пределы интегрирования .
Это достаточно просто. Смотрим на нашу замену и старые пределы интегрирования , .
Сначала подставляем в выражение замены нижний предел интегрирования, то есть, ноль:
Потом подставляем в выражение замены верхний предел интегрирования, то есть, корень из трёх:
Готово. И всего-то лишь…
Продолжаем решение.

(1) В соответствии с заменой записываем новый интеграл с новыми пределами интегрирования .
(2) Это простейший табличный интеграл, интегрируем по таблице. Константу лучше оставить за скобками (можно этого и не делать), чтобы она не мешалась в дальнейших вычислениях. Справа отчеркиваем линию с указанием новых пределов интегрирования – это подготовка для применения формулы Ньютона-Лейбница.
(3) Используем формулу Ньютона-Лейбница  .
.
Ответ стремимся записать в максимально компактном виде, здесь я использовал свойства логарифмов.
Ещё одно отличие от неопределенного интеграла состоит в том, что, после того, как мы провели замену, никаких обратных замен проводить не надо .
А сейчас пара примеров для самостоятельного решения. Какие замены проводить – постарайтесь догадаться самостоятельно.
Пример 6
Вычислить определенный интеграл
Пример 7
Вычислить определенный интеграл
Это примеры для самостоятельного решения. Решения и ответы в конце урока.
И в заключение параграфа пара важных моментов, разбор которых появился благодаря посетителям сайта. Первый из них касается правомерности замены . В некоторых случаях её проводить нельзя! Так, Пример 6, казалось бы, разрешим с помощью универсальной тригонометрической подстановки , однако верхний предел интегрирования («пи») не входит в область определения этого тангенса и поэтому данная подстановка нелегальна! Таким образом, функция-«замена» должна быть непрерывна во всех точках отрезка интегрирования .
В другом электронном письме поступил следующий вопрос: «А нужно ли менять пределы интегрирования, когда мы подводим функцию под знак дифференциала?». Сначала я хотел «отмахнуться от ерунды» и автоматически ответить «конечно, нет», но затем задумался о причине появления такого вопроса и вдруг обнаружил, что информации-то не хватает. А ведь она, пусть и очевидна, но очень важнА:
Если мы подводим функцию под знак дифференциала, то менять пределы интегрирования не нужно
! Почему? Потому что в этом случае нет фактического перехода к новой переменной
. Например:![]()
И здесь подведение гораздо удобнее академичной замены с последующей «росписью» новых пределов интегрирования. Таким образом, если определённый интеграл не очень сложен, то всегда старайтесь подвести функцию под знак дифференциала ! Это быстрее, это компактнее, и это обыденно – в чём вы убедитесь ещё десятки раз!
Большое спасибо за ваши письма!
Метод интегрирования по частям в определенном интеграле
Здесь новизны еще меньше. Все выкладки статьи Интегрирование по частям в неопределенном интеграле
в полной мере справедливы и для определенного интеграла.
Плюсом идёт только одна деталь, в формуле интегрирования по частям добавляются пределы интегрирования:

Формулу Ньютона-Лейбница здесь необходимо применить дважды: для произведения и, после того, как мы возьмем интеграл .
Тип интеграла для примера я опять подобрал такой, который еще нигде не встречался на сайте. Пример не самый простой, но очень и очень познавательный.
Пример 8
Вычислить определенный интеграл
Решаем.
Интегрируем по частям:
У кого возникли трудности с интегралом , загляните на урок Интегралы от тригонометрических функций , там он подробно разобран.

(1) Записываем решение в соответствии с формулой интегрирования по частям.
(2) Для произведения применяем формулу Ньютона-Лейбница. Для оставшегося интеграла используем свойства линейности, разделяя его на два интеграла. Не путаемся в знаках!
(4) Применяем формулу Ньютона-Лейбница для двух найденных первообразных.
Если честно, я недолюбливаю формулу  и, по возможности, … обхожусь вообще без нее! Рассмотрим второй способ решения, с моей точки зрения он более рационален.
и, по возможности, … обхожусь вообще без нее! Рассмотрим второй способ решения, с моей точки зрения он более рационален.
Вычислить определенный интеграл
На первом этапе я нахожу неопределенный интеграл
:
Интегрируем по частям:


Первообразная функция найдена. Константу в данном случае добавлять не имеет смысла.
В чём преимущество такого похода? Не нужно «таскать за собой» пределы интегрирования, действительно, замучаться можно десяток раз записывать мелкие значки пределов интегрирования
На втором этапе я провожу проверку (обычно на черновике).
Тоже логично. Если я неправильно нашел первообразную функцию, то неправильно решу и определенный интеграл. Это лучше выяснить немедленно, дифференцируем ответ:

Получена исходная подынтегральная функция, значит, первообразная функция найдена верно.
Третий этап – применение формулы Ньютона-Лейбница
:
И здесь есть существенная выгода! В «моём» способе решения гораздо меньший риск запутаться в подстановках и вычислениях – формула Ньютона-Лейбница применяется всего лишь один раз. Если чайник решит подобный интеграл по формуле  (первым способом), то стопудово где-нибудь допустит ошибку.
(первым способом), то стопудово где-нибудь допустит ошибку.
Рассмотренный алгоритм решения можно применить для любого определенного интеграла .
Уважаемый студент, распечатай и сохрани:
Что делать, если дан определенный интеграл, который кажется сложным или не сразу понятно, как его решать?
1) Сначала находим неопределенный интеграл (первообразную функцию). Если на первом же этапе случился облом, дальше рыпаться с Ньютоном и Лейбницем бессмысленно. Путь только один – повышать свой уровень знаний и навыков в решении неопределенных интегралов .
2) Проверяем найденную первообразную функцию дифференцированием . Если она найдена неверно, третий шаг будет напрасной тратой времени.
3) Используем формулу Ньютона-Лейбница. Все вычисления проводим ПРЕДЕЛЬНО ВНИМАТЕЛЬНО – тут самое слабое звено задания.
И, на закуску, интеграл для самостоятельного решения.
Пример 9
Вычислить определенный интеграл
Решение и ответ где-то рядом.
Следующий рекомендуемый урок по теме – Как вычислить площадь фигуры с помощью определенного интеграла?
Интегрируем по частям:


Вы точно их прорешали и получили такие ответы? ;-) И на старуху бывает порнуха.
Программные вопросы.
1. Понятие первообразной и неопределенного интеграла.
2. Свойства неопределенного интеграла.
3. Таблица основных интегралов.
4. Методы вычисления неопределенных интегралов.
5. Определенный интеграл.
6. Геометрические приложения определенного интеграла.
Решение типовых примеров .
Неопределенный интеграл.
Интегрирование методом подстановки (замены переменной).
Замена переменной в неопределенном интеграле производится с помощью подстановок двух видов:
1) х = j(t ), где t – новая переменная, а j(t ) – непрерывно дифференцируемая функция; тогда
t = y(x ), где t – новая переменная; в этом случае:
Пример 8.1. Вычислить интеграл
Решение. Вычислим этот интеграл методом подстановки.
Возвращаясь к старой переменной , находим и подставляем в найденное выражение:
Ответ:

Пример 8.2. Вычислить интеграл
Решение. Введем новую переменную , эта подстановка приводит интеграл к такому виду:

Ответ:
![]() .
.
Метод интегрирования по частям.
Пусть U=U(x) и V=V (x ) – функции аргумента х , имеющие непрерывные производные. Тогда возможно интегрирование по частям:
∫UdV = UV - ∫VdU
где V находится по формуле V = ò dV .
Формула интегрирования по частям дает возможность свести вычисление интеграла ∫UdV к вычислению интеграла ∫VdU .
Успех применения формулы интегрирования по частям зависит от правильности выбора множителей U и dV в подынтегральном выражении исходного интеграла. Существуют два полезных правила для такого выбора:
1. Интегралы вида ∫ P(x)e kx dx , ∫ P(x)sinkxdx , ∫ P(x)coskxdx ,
где Р(х) – многочлен, а k – некоторое число, вычисляются по приведенной выше формуле, если положить Р(х)=U.
2. Интегралы вида ∫ P(x)lnxdx , ∫ P(x)arcsinxdx, ∫ P(x)arccosxdx ,
∫ P(x)arctgxdx ,∫ P(x)arcctgxdx , где Р(х) – многочлен. Во всех этих интегралах за и при интегрировании по частям принимают функцию, являющуюся множителем при Р(х), а произведение P(x)dx = dV.
Пример 8.3. Вычислить интеграл
Решение. Согласно формулы интегрирования по частям получаем:
![]()
Ответ:
![]()
Пример 8.4. Вычислить интеграл
Решение. Интегрируя по частям получаем:
=  =
=
Ответ:
![]() .
.
Интегрирование рациональных дробей
Рациональной дробью называется дробь вида где Р(х) и Q(x) – многочлены. Если степень многочлена Q (x ) выше степени многочлена Р (х ), то такая рациональная дробь называется правильной ; в противном случае дробь называется неправильной .
Простейшими дробями I, II, III и IV типов называются рациональные дроби следующего вида:
II. где m – целое число, большее единицы.
III. где квадратный трехчлен x 2 + px + q не имеет
действительных корней.
IV. ![]() где n
– целое число, большее единицы, а
где n
– целое число, большее единицы, а
x 2 + px + q не имеет действительных корней.
Любая правильная рациональная дробь может быть единственным образом представлена в виде суммы простейших рациональных дробей по следующему правилу:
1. Необходимо знаменатель Q (x ) разложить на линейные и квадратные множители, не имеющие действительных корней.
2. Дробь надо разложить на сумму простейших дробей следующим образом:
– каждому сомножителю (х – а ) k разложения Q (x ) отвечает в разложении дроби разложение вида
![]()
где а – корень многочлена Q (x ), а k – кратность этого корня; A 1 , A 2 , …, A k – числа (неопределенные коэффициенты);
– каждому сомножителю разложения Q (x ) – выражение вида
где l – кратность многочлена в разложении Q (x ); B i и C i (i = 1, 2, …, l ) – неопределенные коэффициенты.
3. Полученное равенство необходимо привести к общему знаменателю и, получив равенство двух дробей с одинаковыми знаменателями, приравнять числители.
4. Найти определенные коэффициенты можно двумя способами.
Первый способ . Раскрыть скобки, привести подобные члены и приравнять коэффициенты при одинаковых степенях х .
Второй способ . Не раскрывая скобок, задать аргументу х столько различных значений, сколько имеется неопределенных коэффициентов.
В обоих случаях получаются системы линейных уравнений относительно неопределенных коэффициентов, решая которые получают значения искомых неопределенных коэффициентов.
Замечание. Для нахождения интеграла от неправильной рациональной дроби необходимо, прежде всего выделить из нее целую часть, т.е. представить в виде:
![]()
где M (x ) – многочлен, а – правильная рациональная дробь.
Пример 8.5.
Вычислить интеграл ![]()
Решение. Знаменатель дроби имеет корни х = 2 и х = -5, и его можно разложить на множители следующим образом:
Представим подынтегральную дробь в виде суммы простейших дробей:
![]()
Приведем правую часть равенства к общему знаменателю:
![]()
Приравнивая числители, получим:
Коэффициенты А 1 и А 2 можно найти двумя способами.
Первый способ . Раскроем скобки в правой части последнего равенства и приведем подобные члены:
Приравняем коэффициенты при одинаковых степенях х :
х 1 3 = А 1 + А 2
х 0 8 = 5А 1 - 2А 2
Получим систему двух уравнений с двумя неизвестными:
 , решая которую найдем А
1 = 2, А
2 = 1.
, решая которую найдем А
1 = 2, А
2 = 1.
Следовательно,
![]()
Второй способ . Будем задавать определенные значения х (желательно те значения, при которых знаменатели простейших дробей равны нулю):
| х = 2 х = -5 | |
Таким образом, искомый интеграл
Ответ:
![]()
Пример 8.6.
Вычислить интеграл ![]()
Решение.
Представим подынтегральную дробь в виде суммы простейших дробей. Линейному множителю (х
+ 3) знаменателя этой дроби отвечает дробь а множителю (х
– 2) 2 – сумма простейших дробей вида ![]()
Следовательно, разложение данной дроби на простейшие дроби имеет вид:
![]()
Складывая правую часть равенства и приравнивая числители, получаем
Для вычисления неопределенных коэффициентов будем комбинировать оба изложенных выше способа.
Во первых зададим определенные значения х :

Приравняем коэффициенты при х 2 , получим
![]()
Итак, находим искомый интеграл:

![]()
Ответ:
![]()
![]()
Пример 8.7.
Вычислить интеграл ![]()
Решение. Подынтегральная функция представляет собой неправильную рациональную дробь, поэтому необходимо выделить целую часть, для этого числитель разделим на знаменатель.
В дифференциальном исчислении рассматривались задачи, решение которых требовало отыскания производной данной функции. В ряде случаев приходится решать обратную задачу: по заданной производной отыскивать функцию, которую дифференцировали. Задачи такого рода решаются в разделе математического анализа, называемом интегральным исчислением . Методы интегрального исчисления позволяют решать задачи на вычисление площадей плоских фигур, длин дуг, объемов тел и другие геометрические и физические задачи.
Пример 1. Пусть скорость {v} движения точки в момент времени {t} равна 2t . Найдем выражение для координаты точки в момент времени {t} (точка движется по прямой).
Решение. Известно, что v=\frac{dx}{dt} . Так как в данном случае \frac{dx}{dt}=2t , то ответом к задаче могут быть функции x=t^2; x=t^2+3 и т.д.; в общем виде ответ на поставленный вопрос записывается в виде x=t^2+C , где C - произвольная постоянная.
Из приведенного примера видно, что обратная задача имеет бесконечное множество решений. Чтобы получить определенный закон движения, необходимо знать, например, положение точки в момент времени t=0 . Если при t=0 имеем x=0 , то 0=0+C , и потому C=0 .
Перемещение точки за промежуток времени равно (b^2+C)-(a^2+C)=b^2-a^2 , и, следовательно, оно не зависит от C .
Первообразная функция
Определение 1. Пусть на некотором промежутке X задана функция y=f(x) . Функция y=F(x) называется первообразной для f(x) на этом промежутке, если для всех x\in X
F"(x)=f(x).
Термин "первообразная" был введен французским математиком Ж. Л. Лагранжем (1736-1813).
Следующая теорема позволяет свести нахождение всех первообразных данной функции к отысканию одной из них.
Теорема 1. Если функция y=f(x) имеет на промежутке X первообразную F(x) , то и все функции вида F(x)+C будут для нее первообразными на том же промежутке. Обратно, любая первообразная \Phi(x) для функции y=f(x),\,x\in X , может быть представлена в виде \Phi(x)+C , где F(x) - одна из первообразных функций, а C - произвольная постоянная.
Доказательство. По определению первообразной имеем F"(x)=f(x) . Учитывая, что производная постоянной равна нулю, получаем:
(F(x)+C)"=F"(x)+C"=F"(x)=f(x).
Это и означает, что F(x)+C является первообразной для y=f(x) на промежутке X .
Покажем теперь, что если функция y=f(x) задана на промежутке F и F(x) - одна из первообразных для f(x) , то любая первообразная \Phi(x) может быть представлена в виде \Phi(x)=F(x)+C .
В самом деле, по определению первообразной имеем: \Phi"(x)=f(x) и F"(x)=f(x) . Но две функции, имеющие на промежутке X равные производные, отличаются лишь на постоянное слагаемое. Значит, \Phi(x)=F(x)+C , что и требовалось доказать.
Определения неопределенного и определенного интегралов
Определение 2. Множество всех первообразных для функции y=f(x) на промежутке X называется неопределенным интегралом для f(x) и обозначается .
Функцию y=f(x) называют подынтегральной функцией для \textstyle{\int f(x)\,dx} , а произведение f(x)\,dx - подынтегральным выражением .
Таким образом, \int f(x)\,dx=\{F(x)+C\mid C\in \mathbb{R}\} . На практике принята более короткая запись: \int f(x)\,dx=F(x)+C .
Часто говорят: "взять неопределенный интеграл" или "вычислить неопределенный интеграл", понимая под этим следующее: найти множество всех первообразных для подынтегральной функции.
Мы видели, что если функция имеет хоть одну первообразную, то она имеет бесконечно много первообразных. На практике часто приходится искать разность значений первообразной в точках b и a . Эта разность не зависит от выбора произвольной постоянной C . В самом деле, если \Phi(x)=F(x)+C , то
\Phi(b)-\Phi(b)=(F(b)+C)-(F(a)+C)=F(b)-F(a).
Итак, \Phi(b)-\Phi(b)=F(b)-F(a) , что и требовалось доказать.
Поскольку разность значений первообразной в точках b и a не зависит от того, какую именно первообразную функции y=f(x) мы выбираем, эту разность называют определенным интегралом от функции по отрезку .
Определение 3. Пусть функция y=f(x) задана на отрезке и имеет на нем первообразную y=F(x) . Разность F(b)-F(a) называют определенным интегралом функции f(x) по отрезку и обозначают \textstyle{\int\limits_{a}^{b}f(x)\,dx} . Итак,
\int\limits_{a}^{b}f(x)\,dx=F(b)-F(a).
Разность F(b)-F(a) записывают в виде \Bigl.{F(x)}\Bigr|_{a}^{b} , тогда \textstyle{\int\limits_{a}^{b} f(x)\,dx= \Bigl.{F(x)}\Bigr|_{a}^{b}} . Числа a и b называют пределами интегрирования .
Например, y=\frac{x^3}{3} одна из первообразных для функции y=x^2 . Поэтому
\int\limits_{a}^{b}x^2\,dx=\left.{\frac{x^3}{3}}\right|_{a}^{b}=\frac{b^3}{3}-\frac{a^3}{3}=\frac{b^3-a^3}{3}\,.
Остановимся на геометрическом смысле введенных понятий. Пусть F(x) является первообразной для f(x) . Угловой коэффициент касательной в каждой точке графика функции y=F(x) равен F"(x) , т. е. f(x) . Поэтому задача о нахождении первообразной геометрически означает следующее: зная угловой коэффициент касательной в каждой точке, найти кривую . Так как при параллельном переносе вдоль оси ординат угловой коэффициент касательной в точке с заданной абсциссой не изменяется, то, найдя одну такую кривую, все остальные искомые кривые получают из нее параллельным переносом в направлении оси ординат. Это семейство кривых (рис. 1) и представляет собой геометрическую иллюстрацию неопределенного интеграла.
Определенный интеграл \textstyle{\int\limits_{a}^{b}f(x)\,dx=F(b)-F(a)} показывает изменение ординаты каждой из кривых y=F(x)+C при переходе от точки a к точке b . Так как все эти кривые получаются друг из друга параллельным переносом в направлении оси ординат, то указанное изменение ординаты для всех кривых одно и то же (рис. 2).
Рассмотрим задачи, решение которых сводится к вычислению определенных интегралов.
Задача 1. Пусть точка M движется по прямой и пусть известна скорость v=v(t) движения этой точки в любой момент {x} времени {t} промежутка . Найдем перемещение {s} точки M за этот промежуток времени.
Решение. Мы знаем, что если x=x(t) - закон движения точки, то v(t)=x"(t) . Поэтому x(t) - одна из первообразных для функции v=v(t) . Но перемещение {s} точки M за промежуток времени равно разности ее координат в моменты времени b и a , т.е. равно x(b)-x(a) . Иными словами, это перемещение равно разности значений первообразной для функции v=v(t) в моменты времени b и a . Таким образом, s=\textstyle{\int\limits_{a}^{b}v(t)\,dt} .
Так, например, скорость тела при свободном падении выражают формулой v=gt . В этом случае путь, пройденный падающим телом за b секунд с начала падения, вычисляется так:
S=\int\limits_{0}^{b}gt\,dt= \left.{\frac{gt^2}{2} }\right|_{0}^{b}= \frac{gb^2}{2}\,.
Задача 2. Найдем площадь криволинейной трапеции aA\,Bb , ограниченной осью абсцисс, прямыми x=a и x=b и графиком непрерывной на функции y=f(x) , принимающей на этом отрезке только неотрицательные значения (рис. 3).

Прежде чем переходить к решению задачи, заметим, что здесь мы используем наглядное представление о площади плоской фигуры (более детально вопрос об определении площади).
Решение.
Обозначим через S(x)
площадь криволинейной трапеции aA\,Nx\,(a Дадим абсциссе x
приращение \Delta x
(положим для определенности \Delta x>0
), тогда площадь получит приращение \Delta S
. Обозначим через m
наименьшее значение функции y=f(x)
на отрезке
, а через M
- наибольшее значение той же функции на том же отрезке. Ясно, что тогда m\cdot\Delta x\leqslant\Delta S\leqslant M\cdot\Delta x
, а значит, m\leqslant\frac{\Delta S}{\Delta x}\leqslant M
. Если \Delta x\to 0
, то в силу непрерывности функции y=f(x)
будем иметь: \lim_{\Delta x\to0}m=\lim_{\Delta x\to0}=f(x).
Значит, существует и \lim\frac{\Delta S}{\Delta x}
, причем этот предел равен f(x)
. Таким образом, S"(x)=f(x)
. Полученное равенство означает, что S(x)
- одна из первообразных для функции y=f(x)
. Поскольку прямая x=a
"отсекает" от трапеции aABb
фигуру нулевой площади, то S(a)=0
. С другой стороны, S(b)
- площадь всей криволинейной трапеции aABb
. Значит, искомая площадь S
равна (S(b)-S(a))
, т.е. равна разности значений одной из первообразных для функции y=f(x)
в точках b
и a
. Это означает, что \boldsymbol{S=\int\limits_{a}^{b}f(x)\,dx\,.}
Пример 2.
Найдем площадь фигуры, ограниченной осью абсцисс и одной полуволной синусоиды y=\sin{x}
(рис. 4). Решение.
Искомая площадь S
выражается формулой \textstyle{S= \int\limits_{0}^{\pi}\sin{x}\,dx}
. Одной из первообразных для функции y=\sin{x}
является (-\cos{x})
, так как (-\cos{x})"=\sin{x})
. Значит, S= \int\limits_{0}^{\pi}\sin{x}\,dx=\Bigl.{-\cos{x}}\Bigr|_{0}^{\pi}= -(\cos\pi-\cos0)=-(-1-1)=2.
В заключение данного пункта остановимся на двух свойствах неопределенного интеграла, легко получающихся из определения. 1°.
Дифференциал от неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции:
D\!\left(\int f(x)\,dx\right)= f(x)\,dx,\quad \left(\int f(x)\,dx\right)"=f(x).
Доказательство.
Так как \textstyle{\int f(x)\,dx=F(x)+C}
, где F"(x)=f(x)
, то \textstyle{\left(\int f(x)\,dx\right)"= \bigl(F(x)+C\bigr)"=F"(x)+C"=f(x)}
. Но тогда \textstyle{d\!\left(\int f(x)\,dx\right)= \left(\int f(x)\,dx\right)"dx=f(x)\,dx}
. Это утверждение часто используется для проверки результата интегрирования. Пусть, например, нужно показать, что \int5x\,dx=\frac{5}{2}\,x^2+C\quad (C=\text{const}).
Дифференцируя правую часть равенства, получим подынтегральную функцию: \left(\frac{5}{2}\,x^2+C\right)"=\frac{5}{2}\cdot 2x+0=5x
. Значит, \int5x\,dx=\frac{5}{2}\,x^2+C
. 2°.
Неопределенный интеграл от производной некоторой функции равен этой функции, сложенной с произвольной постоянной:
\int F"(x)\,dx=F(x)+C.
Доказательство.
Так как \bigl(F(x)+C\bigr)"=F"(x)
, то по определению неопределенного интеграла \textstyle{\int F"(x)\,dx=F(x)+C}
, что и требовалось доказать. Учитывая, что F"(x)\,dx=d\bigl(F(x)\bigr)
, свойство 2° можно записать и так: \textstyle{\int d\bigl(F(x)\bigr)=F(x)+C}
. Пользуясь свойством 1° из предыдущего пункта, можно по таблице производных составить таблицу основных интегралов. Например, так как (\sin{x})"=\cos{x}
, то \int\cos{x}\,dx=\sin{x}+C.
. Докажем, что \int\dfrac{1}{x}\,dx=\ln|x|+C
. В самом деле, если x>0
, то |x|=x
и, следовательно, \bigl(\ln|x|\bigr)"=\bigl(\ln{x}\bigr)"=\frac{1}{x}\,
. Если x<0
, то |x|=-x
и, следовательно, \bigl(\ln|x|\bigr)"=\bigl(\ln(-x)\bigr)"= \frac{1}{-x}\cdot(-1)=\frac{1}{x}
. Итак, \bigl(\ln|x|\bigr)"=\frac{1}{x}
, а значит, \int\frac{1}{x}\,dx=\ln|x|+C
. Эту формулу можно применять или на открытом луче (0;+\infty)
, или на открытом луче (-\infty;0)
. Таблица основных интегралов
\begin{aligned}&\boldsymbol{1.}\quad \int 0\,dx=C; &\quad &\boldsymbol{2.}\quad \int 1\,dx=\int dx=x+C;\\ &\boldsymbol{3.}\quad \int x^{a}\,dx=\frac{x^{a+1}}{a+1}+C,~a\ne-1; &\quad &\boldsymbol{4.}\quad \int \frac{dx}{x}=\ln{x}+C;\\ &\boldsymbol{5.}\quad \int \frac{dx}{a^2+x^2}=\frac{1}{a}\operatorname{arctg}\frac{x}{a}+C; &\quad &\boldsymbol{6.}\quad \int \frac{dx}{\sqrt{a^2-x^2}}=\arcsin\frac{x}{a}+C;\\ &\boldsymbol{7.}\quad \int a^x\,dx=\frac{a^x}{\ln a}+C; &\quad &\boldsymbol{8.}\quad \int e^x\,dx=e^x+C;\\ &\boldsymbol{9.}\quad \int \sin{x}\,dx=-\cos{x}+C; &\quad &\boldsymbol{10.}\quad \int \cos{x}\,dx=\sin{x}+C;\\ &\boldsymbol{11.}\quad \int \frac{dx}{\sin^2x}=-\operatorname{ctg}x+C; &\quad &\boldsymbol{12.}\quad \int \frac{dx}{\cos^2x}=\operatorname{tg}x+C;\\ &\boldsymbol{13.}\quad \int \frac{dx}{x^2-a^2}=\frac{1}{2a}\ln\! \left|\frac{x-a}{x+a}\right|+C; &\quad &\boldsymbol{14.}\quad \int \frac{dx}{\sqrt{x^2\pm a^2}}=\ln \bigl|x+\sqrt{x^2\pm a^2}\bigr|+C.\\ \end{aligned}
Заметим, что переменную x
, входящую в эти формулы, можно заменить любой другой. Например, вместо формулы \textstyle{\int\cos{x}\,dx= \sin{x}+C}
можно написать \textstyle{\int\cos{t}\,dt= \sin{t}+C}
и т.д. Пример 3.
Вычислим неопределённые интегралы от различных дробей: \mathsf{1)}~\int\frac{dx}{\sqrt{x}}\,;\quad \mathsf{2)}~\int\frac{dx}{x^2+16}\,;\quad \mathsf{3)}~\int\frac{dx}{x^2-16}\,;\quad \mathsf{4)}~\int\frac{dx}{\sqrt{3-x^2}}\,;\quad \mathsf{5)}~\int\frac{dx}{\sqrt{x^2-3}}\,.
Решение.
1) Воспользуемся формулой 3 из таблицы интегралов: \int\frac{dx}{\sqrt{x}}= \int x^{-1/3}\,dx= \frac{x^{-1/3+1}}{-1/3+1}+C= \frac{3}{2}\,x^{2/3}+C;
2) Воспользуемся формулой 5: \int\frac{dx}{x^2+16}= \int\frac{dx}{x^2+4^2}=\frac{1}{4} \operatorname{arctg}\frac{x}{2}+C;
. 3) Воспользуемся формулой 12: \int\frac{dx}{x^2-16}= \int\frac{dx}{x^2-4^2}= \frac{1}{8}\ln\!\left|\frac{x-4}{x+4}\right|+C;
. 4) Воспользуемся формулой 6: \int\frac{dx}{\sqrt{3-x^2}}= \int\frac{dx}{\sqrt{(\sqrt{3})^2-x^2}}= \arcsin\frac{x}{\sqrt{3}}+C;
. 5) Воспользуемся формулой 13: \int\frac{dx}{\sqrt{x^2-3}}= \ln\Bigl|x+\sqrt{x^2-3}\Bigr|+C.
. Определённым интегралом
от непрерывной функции f
(x
) на конечном отрезке [a
, b
] (где ) называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись Как видно на графиках внизу (приращение первообразной функции обозначено ), определённый
интеграл может быть как положительным, так и отрицательным числом
(Вычисляется
как разность между значением первообразной в верхнем пределе и её же значением в
нижнем пределе, т. е. как F
(b
) - F
(a
)). Числа a
и b
называются соответственно нижним и верхним пределами интегрирования, а отрезок [a
, b
] – отрезком интегрирования. Таким образом, если F
(x
) – какая-нибудь первообразная функция для f
(x
), то, согласно определению, Равенство (38) называется формулой Ньютона-Лейбница
. Разность F
(b
) – F
(a
) кратко записывают так: Поэтому формулу Ньютона-Лейбница будем записывать и так: Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F
(x
) и Ф(х
) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х
) = F
(x
) + C
. Поэтому Тем самым установлено, что на отрезке [a
, b
] приращения всех первообразных функции f
(x
) совпадают. Таким образом, для вычисления
определённого интеграла необходимо найти любую первообразную подынтегральной
функции, т.е. сначала следует найти неопределённый интеграл. Постоянная
С
из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница:
в первообразную функцию подставляется значение верхнего предела
b
, далее - значение
нижнего предела
a
и вычисляется разность
F(b) - F(a)
. Полученное число и будет
определённым интегралом.
. При a
= b
по определению принимается Пример 1.
Решение. Сначала найдём неопределённый интеграл: Применяя формулу Ньютона-Лейбница к первообразной (при С
= 0), получим Однако при вычислении определённого интеграла лучше не находить отдельно первообразную, а сразу записывать интеграл в виде (39). Пример 2.
Вычислить определённый интеграл Решение. Используя формулу Теорема 2.
Величина определённого интеграла не зависит от обозначения переменной интегрирования
, т.е. Пусть F
(x
) – первообразная для f
(x
). Для f
(t
) первообразной служит та же функция F
(t
), в которой лишь иначе обозначена независимая переменная. Следовательно, На основании формулы (39) последнее равенство означает равенство интегралов Теорема 3.
Постоянный множитель можно выносить за знак определённого интеграла
, т.е. Теорема 4.
Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций
, т.е. Теорема 5.
Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям
, т.е. если Теорема 6.
При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак
, т.е. Теорема 7
(теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке внутри его
, т.е. Теорема 8.
Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если
Теорема 9.
Если верхний предел интегрирования больше нижнего и функции и непрерывны, то неравенство
можно почленно интегрировать
, т.е. Свойства определённого интеграла позволяют упрощать непосредственное вычисление интегралов. Пример 5.
Вычислить определённый интеграл Используя теоремы 4 и 3, а при нахождении первообразных – табличные интегралы (7) и (6), получим Пусть f
(x
) – непрерывная на отрезке [a
, b
] функция, а F
(x
) – её первообразная. Рассмотрим определённый интеграл а через t
обозначена переменная интегрирования, чтобы не путать её с верхней границей. При изменении х
меняется и опредёленный интеграл (47), т.е. он является функцией верхнего предела интегрирования х
, которую обозначим через Ф
(х
), т.е. Докажем, что функция Ф
(х
) является первообразной для f
(x
) = f
(t
). Действительно, дифференцируя Ф
(х
), получим так как F
(x
) – первообразная для f
(x
), а F
(a
) – постояная величина. Функция Ф
(х
) – одна из бесконечного множества первообразных для f
(x
), а именно та, которая при x
= a
обращается в нуль. Это утверждение получается, если в равенстве (48) положить x
= a
и воспользоваться теоремой 1 предыдущего параграфа. где, по определению, F
(x
) – первообразная для f
(x
). Если в подынтегральном выражении произвести замену переменной то в соответствии с формулой (16) можно записать В этом выражении первообразная функция для В самом деле, её производная, согласно правилу дифференцирования сложной функции
, равна Пусть α и β – значения переменной t
, при которых функция принимает соответственно значения a
и b
, т.е. Но, согласно формуле Ньютона-Лейбница, разность F
(b
) – F
(a
) есть
Таблица основных интегралов
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

![]() (38)
(38)![]() (39)
(39)
![]()
![]()
![]()
Свойства определённого интеграла
![]() (40)
(40)![]()
![]() (41)
(41)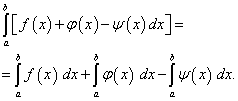 (42)
(42)![]() (43)
(43)![]() (44)
(44)![]() (45)
(45)
![]() (46)
(46)![]()

Определённый интеграл с переменным верхним пределом
![]() (47)
(47)![]() (48)
(48)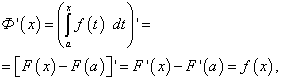
Вычисление определённых интегралов методом интегрирования по частям и методом замены переменной
![]()


