Секущая прямая
Окружность - геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.
Данная точка (O) называется центром окружности
.
Радиус окружности
- это отрезок, соединяющий центр с какой-либо точкой окружности. Все радиусы имеют одну и ту же длину (по определению).
Хорда
- отрезок, соединяющий две точки окружности. Хорда, проходящая через центр окружности, называется диаметром
. Центр окружности является серединой любого диаметра.
Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности
. Дуга называется полуокружностью
, если отрезок, соединяющий её концы, является диаметром.
Длина единичной полуокружности обозначается через π
.
Сумма градусных мер двух дуг окружности с общими концами равна 360º
.
Часть плоскости, ограниченная окружностью, называется кругом
.
Круговой сектор
- часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга. Дуга, которая ограничивает сектор, называется дугой сектора
.
Две окружности, имеющие общий центр, называются концентрическими
.
Две окружности, пересекающиеся под прямым углом, называются ортогональными
.
Взаимное расположение прямой и окружности
- Если расстояние от центра окружности до прямой меньше радиуса окружности (d), то прямая и окружность имеют две общие точки. В этом случае прямая называется секущей по отношению к окружности.
- Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку. Такая прямая называется касательной к окружности , а их общая точка называется точкой касания прямой и окружности .
- Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек .
Центральные и вписанные углы
Центральный угол
- это угол с вершиной в центре окружности.
Вписанный угол
- угол, вершина которого лежит на окружности, а стороны пересекают окружность.
Теорема о вписанном угле
Вписанный угол измеряется половиной дуги, на которую он опирается.
- Следствие 1.
Вписанные углы, опирающиеся на одну и ту же дугу, равны. - Следствие 2.
Вписанный угол, опирающийся на полуокружность - прямой.
Теорема о произведении отрезков пересекающихся хорд.
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Основные формулы
- Длина окружности:
- Длина дуги окружности:
- Диаметр:
- Длина дуги окружности:
где α - градусная мера длины дуги окружности)
- Площадь круга:
- Площадь кругового сектора:
Уравнение окружности
- В прямоугольной системе координат уравнение окружности радиуса r с центром в точке C (x о;y о) имеет вид:
- Уравнение окружности радиуса r с центром в начале координат имеет вид:
Геометрическое место точек. Срединный перпендикуляр . Биссектриса угла.
Окружность. Круг. Центр окружности. Радиус. Дуга. Секущая. Хорда.
Диаметр. Касательная и её свойства. Сегмент. Сектор. Углы в круге.
Длина дуги. Радиан. Соотношения между элементами круга.
Геометрическое местоточек – этомножество всех точек,удовлетворя ющихопределённым заданным условиям.
П р и м е р 1. Срединный перпендикуляр любого отрезка есть геометрическое
место точек (т.е. множество всех точек), равноудалён ных от
концов этого отрезка. Пусть PO AB и AO = OB:

Тогда, расстояния от любой точки P, лежащей на срединном перпендикуляре PO, до концов A и B отрезка AB одинаковы и равны d .
Таким образом, каждая точка срединного перпендикуляра отрезка обладает следующим свойством: она равноудалена от концов отрезка.
П р и м е р 2. Биссектриса угла есть геометрическое место точек, равноудалённых от его сторон .
П р и м е р 3. Окружность есть геометрическое место точек (т.е. множе ство
всех точек), равноудалённых от её центра (на рис. пока зана одна
из этих точек – А).
Окружность - это геометрическое место точек (т.е. множество всех точек) на плоскости , равноудалённых от одной точки, называемой центром окружности. Отрезок, соединяющий центр окружности с какой-либо её точкой, называется радиусом и обозначается r или R . Часть плоскости, ограниченная окружностью, называется кругом . Часть окружности (
Am B , рис.39 ) называется дугой. Прямая PQ , проходящая через точки M и N окружности ( рис.39 ), называется секущей, а её отрезок MN , лежащий внутри окружности - хордой.
Хорда, проходящая через центр круга (например,
BC, рис.39), называется диаметром и обозначается d или D . Диаметр – это наибольшая хорда, равная двум радиусам (d = 2 r ).
Касательная. Предположим, секущая PQ (рис.40) проходит через точки K и M окружности. Предположим также, что точка M движется вдоль окружности, приближаясь к точке K. Тогда секущая PQ будет менять своё положение, вращаясь вокруг точки K. По мере приближения точки M к точке K секущая PQ будет стремиться к некоторому предельному положению АВ. Прямая AB называется касательной к окружности в точке K. Точка K называется точкой касания. Касательная и окружность имеют только одну общую точку – точку касания.
Свойства касательной.
1) К асательная к окружности перпендикулярна к радиусу, проведенному в точку касания ( AB OK, рис.40) .
2) Из точки, лежащей вне круга, можно провести две касательные к
одной и той же окружности; их отрезки равны (рис.41).
Сегмент – это часть круга, ограниченная дугой ACB и соответствующей хордой AB (рис.42). Длина перпендикуляра CD, проведенного из середины хорды AB до пересечения с дугой ACB, называется высотой сегмента.
Сектор – эточасть круга,ограниченная дугой Am Bи двумя радиусами OAи OB, проведенными к концам этой дуги (рис.43).

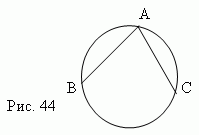
Углы в круге. Центральный угол – угол, образованный двумя радиусами ( AOB, рис.43). Вписанный угол – угол, образованный двумя хордами AB и AC, проведенными из их одной общей точки (BA C, рис.44). Описанный угол – угол, образованный двумя касательными AB и AC, проведенными из одной общей точки ( BAC, рис.41).
Длина дуги окружности пропорциональна её радиусу r и соответствующему центральному углу :
l = r
Таким образом, если мы знаем длину дуги
l и радиус r , то величина соответствующего центрального угла может быть определена их отношением: = l / r .Эта формула является основой для определения радианного измерения углов. Так, если l = r , то = 1, и мы говорим, что угол равен 1 радиану (это обозначается: = 1 рад ). Таким образом, мы имеем следующее определение радиана как единицы измерения углов: радиан – это центральный угол ( AOB, рис.43), у которого длина дуги равна её радиусу (Am B = AO , рис.43). Итак, радианная мера любого угла – это отношение длины дуги, проведенной произвольным радиусом и заключённой между сторонами этого угла, к её радиусу. В частности, в соответствии с формулой длины дуги, длина окружности C может быть выражена следующим образом:
где определяется как отношение C к диаметру круга 2 r :
= C / 2 r .
Иррациональное число; его приближённое значение 3.1415926…
С другой стороны, 2- это круговой угол окружности, который в градусной системе измерения равен 360º. На практике часто случается, что как радиус дуги, так и угол неизвестны. В этом случае длина дуги может быть вычислена по приближённой формуле Гюйгенса:
p 2l + (2l – L ) / 3 ,
где (см. рис.42): p – длина дуги ACB ; l – длина хорды AC ; L – длина хорды AB . Если дуга содержит не более чем 60 º , относительная погрешность этой формулы не превышает 0.5%.
Соотношения между элементами круга. Вписанный угол ( ABC , рис.45) равен половине центрального угла , опирающегося на ту же дугу AmC ( AOC , рис.45) . Поэтому, все вписанные углы (рис.45), опирающиеся на одну и ту же дугу ( Am C , рис.45), равны. А так как центральный угол содержит тоже количество градусов, чтои его дуга ( Am C ,рис.45), то любой вписанный угол измеряется половиной дуги, на которую он опирается (внашем случае Am C ).

Все вписанные углы, опирающиеся на полукруг (APB, AQB, …, рис.46 ), прямые (Докажите это, пожалуйста!).
Угол (AOD, рис.47 ), образованный двумя хордами (ABи CD), измеряет ся полусуммой дуг, заключённых между его сторонами: (An D + Cm B) / 2 .

Угол (AOD, рис.48 ), образованный двумя секущими (AOи OD), измеряется полуразностью дуг, заключённых между его сторонами: (An D– Bm C ) / 2. секущей (COи BO), измеряется полуразностью дуг,заключённых между его сторонами: ( Bm C– Cn D ) / 2 .

Описанный угол (AOC, рис.50 ), образованный двумя касательными (COи AO), измеряется полуразностью дуг,заключенных между его сторонами: ( ABC– CDA) / 2 .
Произведения отрезков хорд ( AB и CD , рис.51 или рис.52), на которые они делятся точкой пересечения, равны: AO · BO = CO · DO .
К вадрат касательной равен произведению секущей на её внешнюю часть ( рис.50 ) : OA 2 = OB · O D (докажите!). Это свойство можно рассматривать как частный случай рис.52.

Хорда (AB, рис.53), перпендикулярная диаметру (CD), делится в их точке пересечения O пополам: AO = OB.
( Попробуйте доказать это! ).
И круг - геометрические фигуры, взаимосвязанные между собой. есть граничная ломаная линия (кривая) круга ,
Определение. Окружность - замкнутая кривая, каждая точка которой равноудалена от точки, называемой центром окружности.
Для построения окружности выбирается произвольная точка О, принятая за центр окружности, и с помощью циркуля проводится замкнутая линия.
Если точку О центра окружности соединить с произвольными точками на окружности, то все полученные отрезки будут между собой равны, и называются такие отрезки радиусами, сокращенно обозначаются латинской маленькой или большой буквой «эр» (r или R ). Радиусов в окружности можно провести столько же, сколько точек имеет длина окружности.
Отрезок, соединяющий две точки окружности и проходящий через ее центр, называется диаметром. Диаметр состоит из двух радиусов , лежащих на одной прямой. Диаметр обозначается латинской маленькой или большой буквой «дэ» (d или D ).
Правило. Диаметр окружности равен двум ее радиусам .
d = 2r
D = 2R
Длина окружности вычисляется по формуле и зависит от радиуса (диаметра) окружности. В формуле присутствует число ¶, которое показывает во сколько раз длина окружности больше, чем ее диаметр. Число ¶ имеет бесконечное число знаков после запятой. Для вычислений принято ¶ = 3,14.
Длина окружности обозначается латинской большой буквой «цэ» (C ). Длина окружности пропорциональна ее диаметру. Формулы для расчета длины окружности по ее радиусу и диаметру:
C = ¶d
C = 2¶r
- Примеры
- Дано: d = 100 см.
- Длина окружности: C = 3,14 * 100 см = 314 см
- Дано: d = 25 мм.
- Длина окружности: С = 2 * 3,14 * 25 = 157 мм
Секущая окружности и дуга окружности
Всякая секущая (прямая линия) пересекает окружность в двух точках и делит ее на две дуги. Величина дуги окружности зависит от расстояния между центром и секущей и измеряется по замкнутой кривой от первой точки пересечения секущей с окружностью до второй.
Дуги окружности делятся секущей на большую и малую, если секущая не совпадает с диаметром, и на две равные дуги, если секущая проходит по диаметру окружности.
Если секущая проходит через центр окружности, то ее отрезок, расположенный между точками пересечения с окружностью, есть диаметр окружности, или самая большая хорда окружности.
Чем дальше секущая расположена от центра окружности, тем меньше градусная мера меньшей дуги окружности и больше - большей дуги окружности, а отрезок секущей, называемый хордой , уменьшается по мере удаления секущей от центра окружности.

Определение. Кругом называется часть плоскости, лежащая внутри окружности.
Центр, радиус, диаметр окружности являются одновременно центром, радиусом и диаметром соответствующего круга.
Так как круг - это часть плоскости, то одним из его параметров является площадь.
Правило. Площадь круга (S ) равна произведению квадрата радиуса (r 2 ) на число ¶.

- Примеры
- Дано: r = 100 см
- Площадь круга:
- S = 3,14 * 100 см * 100 см = 31 400 см 2 ≈ 3м 2
- Дано: d = 50 мм
- Площадь круга:
- S = ¼ * 3,14 * 50 мм * 50 мм = 1 963 мм 2 ≈ 20 см 2
Если в круге провести два радиуса к разным точкам окружности, то образуется две части круга, которые называется секторами . Если в круге провести хорду, то часть плоскости между дугой и хордой называется сегментом окружности .
Вопрос 3. Какая прямая называется секущей двух данных прямых? Ответ: Секущей называется прямая, пересекающая две данные прямые.
Картинка 13 из презентации «Задачи о параллельных прямых» к урокам геометрии на тему «Параллельность»Размеры: 960 х 720 пикселей, формат: jpg. Чтобы бесплатно скачать картинку для урока геометрии, щёлкните по изображению правой кнопкой мышки и нажмите «Сохранить изображение как...». Для показа картинок на уроке Вы также можете бесплатно скачать презентацию «Задачи о параллельных прямых.ppt» целиком со всеми картинками в zip-архиве. Размер архива - 118 КБ.
Скачать презентациюПараллельность
«Геометрия «Аксиома параллельных прямых»» - Можно ли это доказать. Закончи предложение. Математическое утверждение. Через любые две точки проходит прямая, и притом только одна. Проверка задания. Через точку, не лежащую на данной прямой, проходит только одна прямая. Сколько отрезков данной длины можно отложить от начала луча. Найдите соответствие.
«Задачи о параллельных прямых» - Разность двух внутренних односторонних углов. Назовите внутренние односторонние углы. Найдите все углы. Какая прямая называется секущей. Сумма внутренних накрест лежащих углов. Две прямые на плоскости называются параллельными. Могут ли прямые АВ и CD быть параллельными. Какие прямые называются параллельными.
«Геометрия Параллельные прямые» - Каково взаимное расположение отрезков АВ, СД, МК? Дайте определение параллельных отрезков и параллельных лучей. Как могут быть расположены две прямые на плоскости? Сделайте вывод. Параллельность прямых a и b обозначается a ?? b . Признаки параллельности двух прямых: Параллельные прямые. Прямые a и b перпенди- кулярны прямой с.
«Параллельные прямые» - Признаки параллельности двух прямых. Отсюда следует, а и в перпендикулярны к прямой АВ и, следовательно, параллельны. Параллельные прямые. Признаки параллельности прямых. Ч.Т.Д. Доказательство: Две прямые имеют одну общую точку, то есть пересекаются.
Окружностью называется фигура, состоящая из всех точек плоскости, находящихся от данной точки на данном расстоянии. Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, - радиусом окружности.
Часть плоскости, ограниченная окружностью называется кругом.
Круговым сектором или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Сегментом называется часть круга, ограниченная дугой и стягивающей ее хордой.
Основные термины
Касательная
Прямая, имеющая с только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
Свойства касательной
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Хорда
Отрезок, соединяющий две точки окружности, называется ее хордой. Хорда, проходящая через центр окружности, называется диаметром.
Свойства хорд
Диаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде.
Дуги, заключенные между параллельными хордами, равны.
Если две хорды окружности, AB и CD пересекаются в точке M , то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM MB = CM MD.
Свойства окружности
Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку (касательная ); иметь с ней две общие точки (секущая ).
Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
Точка касания двух окружностей лежит на линии, соединяющей их центры.

Теорема о касательной и секущей
Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть: MC 2 = MA MB .
Теорема о секущих
Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть.MA MB = MC MD.
Углы в окружности
Центральным углом в окружности называется плоский угол с вершиной в ее центре.
Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом.
Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности. Мерой дуги может служить мера соответствующего ей центрального угла.
Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.
Свойства углов, связанных с окружностью
Вписанный угол либо равен половине соответствующего ему центрального угла, либо дополняет половину этого угла до 180°.

Углы, вписанные в одну окружность и опирающиеся на одну и ту же дугу, равны.
Вписанный угол, опирающийся на диаметр, равен 90°.
Угол, образованный касательной к окружности и секущей, проведенной через точку касания, равен половине дуги, заключенной между его сторонами.

Длины и площади
Длина окружности C радиуса R вычисляется по формуле:
C = 2 R .
Площадь S круга радиуса R вычисляется по формуле:
S = R 2 .
Вписанные и описанные окружности
Окружность и
треугольник
центр вписанной окружности - точка пересечения биссектрис треугольника, ее радиус r вычисляется по формуле:
r = ,
где S - площадь треугольника, а - полупериметр;
R = ,
R = ;
здесь a, b, c - стороны треугольника, - угол, лежащий против стороны a , S - площадь треугольника;
центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы;
центр описанной и вписанной окружностей треугольника совпадают только в том случае, когда этот треугольник - правильный.
Окружность и четырехугольники
около выпуклого четырехугольника можно описать окружность тогда и только тогда, когда сумма его внутренних противоположных углов равна 180°:
180°;
в четырехугольник можно вписать окружность тогда и только тогда, когда у него равны суммы противоположных сторон:
a + c = b + d ;
около параллелограмма можно описать окружность тогда и только тогда, когда он является прямоугольником;
около трапеции можно описать окружность тогда и только тогда, когда эта трапеция - равнобедренная; центр окружности лежит на пересечении оси симметрии трапеции c серединным перпендикуляром к боковой стороне;
в параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом.
